363. Max Sum of Rectangle No Larger Than K


Description
Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.
It is guaranteed that there will be a rectangle with a sum no larger than k.
Example 1:
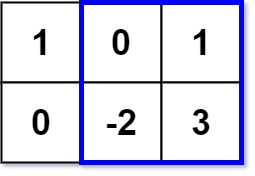
Input: matrix = [[1,0,1],[0,-2,3]], k = 2 Output: 2 Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).
Example 2:
Input: matrix = [[2,2,-1]], k = 3 Output: 3
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-100 <= matrix[i][j] <= 100-105 <= k <= 105
Follow up: What if the number of rows is much larger than the number of columns?
Solution
max-sum-of-rectangle-no-larger-than-k.py
from sortedcontainers import SortedList
class Solution:
def maxSumSubmatrix(self, matrix: List[List[int]], k: int) -> int:
rows, cols = len(matrix), len(matrix[0])
maxSize = min(rows, cols)
prefix = [[0] * (cols + 1) for _ in range(rows + 1)]
for i in range(rows):
for j in range(cols):
prefix[i + 1][j + 1] += prefix[i + 1][j] + matrix[i][j]
for i in range(rows):
for j in range(cols):
prefix[i + 1][j + 1] += prefix[i][j + 1]
res = float('-inf')
for row1 in range(rows):
for row2 in range(row1, rows):
sl = SortedList()
sl.add(0)
for j in range(cols):
curr = prefix[row2 + 1][j + 1] - prefix[row1][j + 1]
target = curr - k
index = sl.bisect_left(target)
if 0 <= index < len(sl):
res = max(res, curr - sl[index])
sl.add(curr)
return res