407. Trapping Rain Water II

,%20Matrix-orange.svg)
Description
Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.
Example 1:
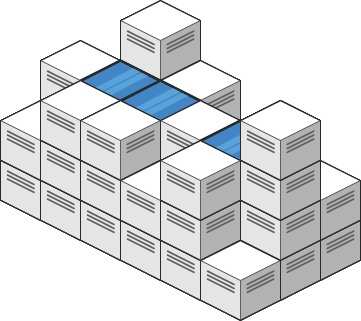
Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] Output: 4 Explanation: After the rain, water is trapped between the blocks. We have two small ponds 1 and 3 units trapped. The total volume of water trapped is 4.
Example 2:
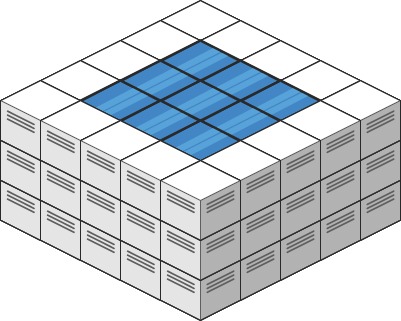
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]] Output: 10
Constraints:
m == heightMap.lengthn == heightMap[i].length1 <= m, n <= 2000 <= heightMap[i][j] <= 2 * 104
Solution
trapping-rain-water-ii.py
class Solution:
def trapRainWater(self, heights: List[List[int]]) -> int:
rows, cols = len(heights), len(heights[0])
res = 0
visited = [[False] * cols for _ in range(rows)]
pq = []
for x in range(0, rows):
visited[x][0] = True
heappush(pq, (heights[x][0], x, 0))
visited[x][cols - 1] = True
heappush(pq, (heights[x][cols - 1], x, cols - 1))
for y in range(cols):
visited[0][y] = True
heappush(pq, (heights[0][y], 0, y))
visited[rows - 1][y] = True
heappush(pq, (heights[rows - 1][y], rows - 1, y))
while pq:
h, x, y = heappop(pq)
for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
if 0 <= dx < rows and 0 <= dy < cols and not visited[dx][dy]:
visited[dx][dy] = True
res += max(0, h - heights[dx][dy])
heappush(pq, (max(h, heights[dx][dy]), dx, dy))
return res