662. Maximum Width of Binary Tree


Description
Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is guaranteed that the answer will in the range of a 32-bit signed integer.
Example 1:
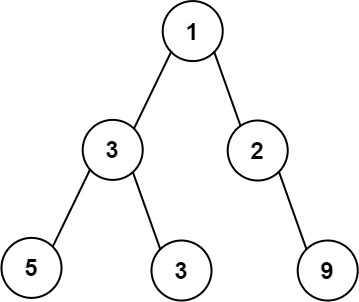
Input: root = [1,3,2,5,3,null,9] Output: 4 Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).
Example 2:
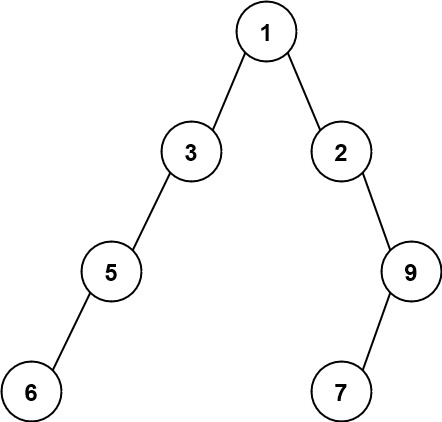
Input: root = [1,3,2,5,null,null,9,6,null,7] Output: 7 Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
Example 3:
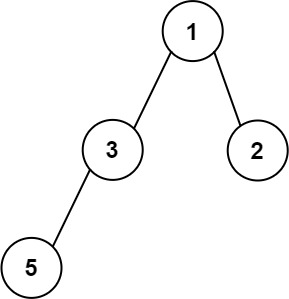
Input: root = [1,3,2,5] Output: 2 Explanation: The maximum width exists in the second level with length 2 (3,2).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
Solution
maximum-width-of-binary-tree.py
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
queue = deque([root])
mp = defaultdict(int)
mp[root] = 1
res = 1
while queue:
n = len(queue)
start = end = -1
for index in range(n):
node = queue.popleft()
if index == 0:
start = mp[node]
elif index == n - 1:
end = mp[node]
if node.left:
queue.append(node.left)
mp[node.left] = 2 * mp[node]
if node.right:
queue.append(node.right)
mp[node.right] = 2 * mp[node] + 1
res = max(res, end - start + 1)
return res