684. Redundant Connection


Description
In this problem, a tree is an undirected graph that is connected and has no cycles.
You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.
Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.
Example 1:
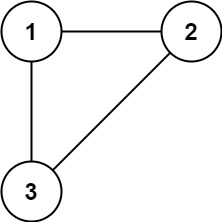
Input: edges = [[1,2],[1,3],[2,3]] Output: [2,3]
Example 2:
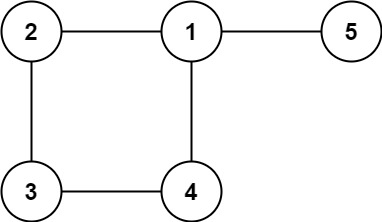
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]] Output: [1,4]
Constraints:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ai < bi <= edges.lengthai != bi- There are no repeated edges.
- The given graph is connected.
Solution
redundant-connection.py
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges)
parent = [i for i in range(n)]
def ufind(x):
if parent[x] != x:
parent[x] = ufind(parent[x])
return parent[x]
def uunion(x, y):
px = ufind(x)
py = ufind(y)
parent[px] = py
for a, b in edges:
a -= 1; b -= 1
if ufind(a) == ufind(b):
return [a + 1, b + 1]
uunion(a, b)