741. Cherry Pickup


Description
You are given an n x n grid representing a field of cherries, each cell is one of three possible integers.
0means the cell is empty, so you can pass through,1means the cell contains a cherry that you can pick up and pass through, or-1means the cell contains a thorn that blocks your way.
Return the maximum number of cherries you can collect by following the rules below:
- Starting at the position
(0, 0)and reaching(n - 1, n - 1)by moving right or down through valid path cells (cells with value0or1). - After reaching
(n - 1, n - 1), returning to(0, 0)by moving left or up through valid path cells. - When passing through a path cell containing a cherry, you pick it up, and the cell becomes an empty cell
0. - If there is no valid path between
(0, 0)and(n - 1, n - 1), then no cherries can be collected.
Example 1:
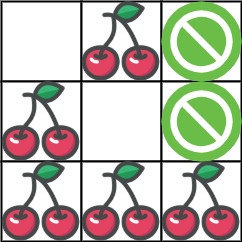
Input: grid = [[0,1,-1],[1,0,-1],[1,1,1]] Output: 5 Explanation: The player started at (0, 0) and went down, down, right right to reach (2, 2). 4 cherries were picked up during this single trip, and the matrix becomes [[0,1,-1],[0,0,-1],[0,0,0]]. Then, the player went left, up, up, left to return home, picking up one more cherry. The total number of cherries picked up is 5, and this is the maximum possible.
Example 2:
Input: grid = [[1,1,-1],[1,-1,1],[-1,1,1]] Output: 0
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 50grid[i][j]is-1,0, or1.grid[0][0] != -1grid[n - 1][n - 1] != -1
Solution
cherry-pickup.py
class Solution:
def cherryPickup(self, grid: List[List[int]]) -> int:
n = len(grid)
directions = [(1, 0), (0, 1)]
@cache
def go(r1, c1, r2, c2):
if r1 == r2 == c1 == c2 == n - 1: return 0
res = float('-inf')
for dx1, dy1 in directions:
R1, C1 = r1 + dx1, c1 + dy1
if not (0 <= R1 < n and 0 <= C1 < n and grid[R1][C1] != -1): continue
for dx2, dy2 in directions:
R2, C2 = r2 + dx2, c2 + dy2
if 0 <= R2 < n and 0 <= C2 < n and grid[R2][C2] != -1:
cherries = grid[R1][C1] + (grid[R2][C2] * int((R1, C1) != (R2, C2)))
res = max(res, go(R1, C1, R2, C2) + cherries)
return res
return max(0, go(0, 0, 0, 0) + grid[0][0])