766. Toeplitz Matrix


Description
Given an m x n matrix, return true if the matrix is Toeplitz. Otherwise, return false.
A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same elements.
Example 1:
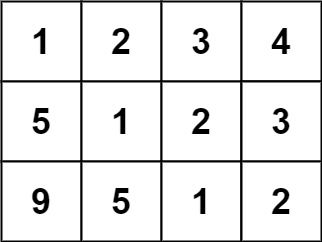
Input: matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]] Output: true Explanation: In the above grid, the diagonals are: "[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]". In each diagonal all elements are the same, so the answer is True.
Example 2:
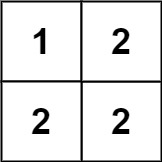
Input: matrix = [[1,2],[2,2]] Output: false Explanation: The diagonal "[1, 2]" has different elements.
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200 <= matrix[i][j] <= 99
Follow up:
- What if the
matrixis stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once? - What if the
matrixis so large that you can only load up a partial row into the memory at once?
Solution
toeplitz-matrix.py
class Solution:
def isToeplitzMatrix(self, matrix: List[List[int]]) -> bool:
rows, cols = len(matrix), len(matrix[0])
for j in range(cols):
curr = matrix[0][j]
ki, kj = 1, j + 1
while ki < rows and kj < cols:
if matrix[ki][kj] != curr:
return False
ki += 1
kj += 1
for i in range(rows):
curr = matrix[i][0]
ki, kj = i + 1, 1
while ki < rows and kj < cols:
if matrix[ki][kj] != curr:
return False
ki += 1
kj += 1
return True