986. Interval List Intersections


Description
You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.
A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.
The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].
Example 1:
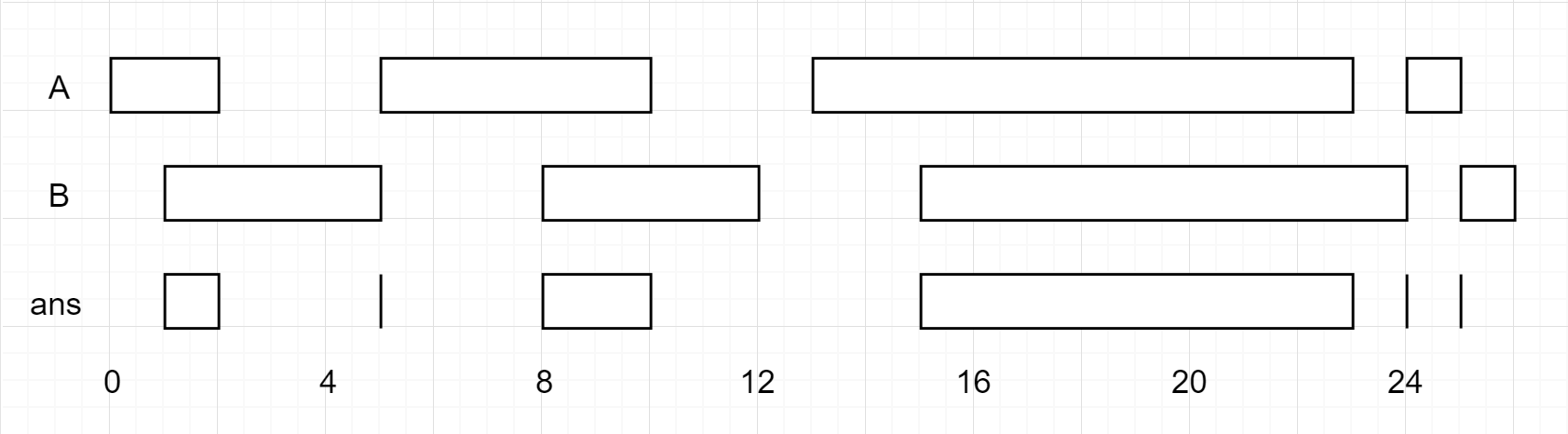
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]] Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Example 2:
Input: firstList = [[1,3],[5,9]], secondList = [] Output: []
Constraints:
0 <= firstList.length, secondList.length <= 1000firstList.length + secondList.length >= 10 <= starti < endi <= 109endi < starti+10 <= startj < endj <= 109endj < startj+1
Solution
interval-list-intersections.py
class Solution:
def intervalIntersection(self, firstList: List[List[int]], secondList: List[List[int]]) -> List[List[int]]:
i = j = 0
n, m = len(firstList), len(secondList)
res = []
while i < n and j < m:
s1, e1 = firstList[i]
s2, e2 = secondList[j]
s, e = max(s1, s2), min(e1, e2)
if s <= e:
res.append([s, e])
if e1 <= e2:
i += 1
else:
j += 1
return res