1008. Construct Binary Search Tree from Preorder Traversal


Description
Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.
A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.
A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.
Example 1:
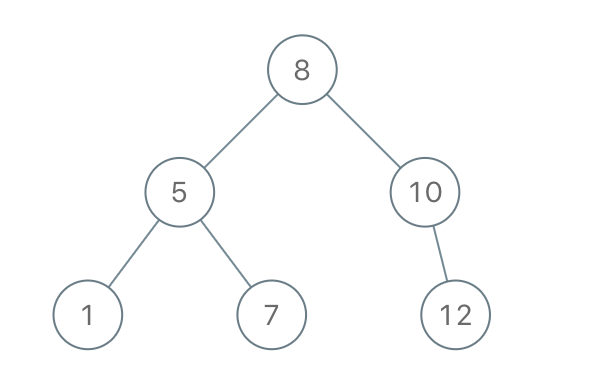
Input: preorder = [8,5,1,7,10,12] Output: [8,5,10,1,7,null,12]
Example 2:
Input: preorder = [1,3] Output: [1,null,3]
Constraints:
1 <= preorder.length <= 1001 <= preorder[i] <= 1000- All the values of
preorderare unique.
Solution
construct-binary-search-tree-from-preorder-traversal.py
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:
def go(A, bound = float('inf')):
if not A or A[-1] > bound: return None
node = TreeNode(A.pop())
node.left = go(A, node.val)
node.right = go(A, bound)
return node
return go(preorder[::-1])