1074. Number of Submatrices That Sum to Target


Description
Given a matrix and a target, return the number of non-empty submatrices that sum to target.
A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.
Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.
Example 1:
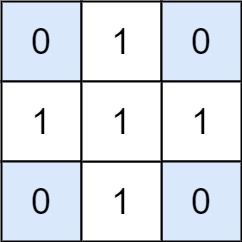
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0 Output: 4 Explanation: The four 1x1 submatrices that only contain 0.
Example 2:
Input: matrix = [[1,-1],[-1,1]], target = 0 Output: 5 Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.
Example 3:
Input: matrix = [[904]], target = 0 Output: 0
Constraints:
1 <= matrix.length <= 1001 <= matrix[0].length <= 100-1000 <= matrix[i] <= 1000-10^8 <= target <= 10^8
Solution
number-of-submatrices-that-sum-to-target.py
class Solution:
def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
rows, cols = len(matrix), len(matrix[0])
for i in range(rows):
for j in range(1, cols):
matrix[i][j] += matrix[i][j - 1]
res = 0
for i in range(cols):
for j in range(i, cols):
mp = collections.defaultdict(int)
curr, mp[0] = 0, 1
for k in range(rows):
curr += matrix[k][j] - (matrix[k][i - 1] if i > 0 else 0)
res += mp[curr - target]
mp[curr] += 1
return res