1080. Insufficient Nodes in Root to Leaf Paths


Description
Given the root of a binary tree and an integer limit, delete all insufficient nodes in the tree simultaneously, and return the root of the resulting binary tree.
A node is insufficient if every root to leaf path intersecting this node has a sum strictly less than limit.
A leaf is a node with no children.
Example 1:
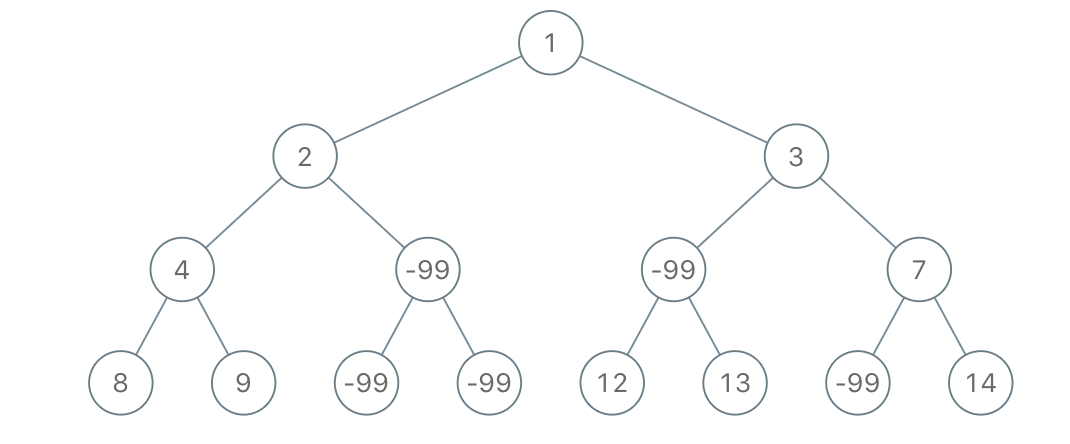
Input: root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1 Output: [1,2,3,4,null,null,7,8,9,null,14]
Example 2:
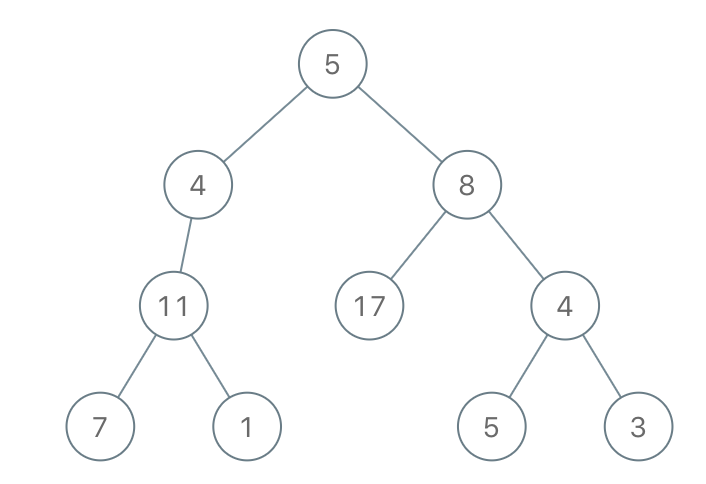
Input: root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22 Output: [5,4,8,11,null,17,4,7,null,null,null,5]
Example 3:
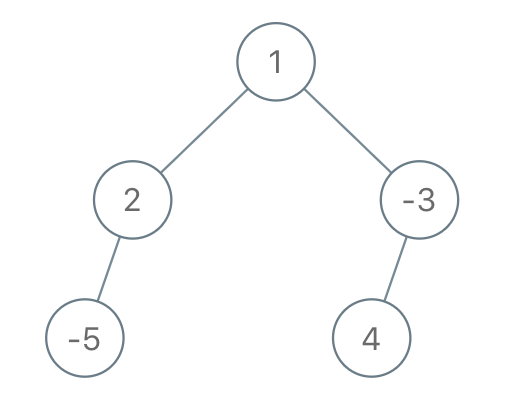
Input: root = [1,2,-3,-5,null,4,null], limit = -1 Output: [1,null,-3,4]
Constraints:
- The number of nodes in the tree is in the range
[1, 5000]. -105 <= Node.val <= 105-109 <= limit <= 109
Solution
insufficient-nodes-in-root-to-leaf-paths.py
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sufficientSubset(self, root: TreeNode, limit: int) -> TreeNode:
if root.left == root.right:
return None if root.val < limit else root
if root.left:
root.left = self.sufficientSubset(root.left, limit - root.val)
if root.right:
root.right = self.sufficientSubset(root.right, limit - root.val)
return root if root.left or root.right else None