1091. Shortest Path in Binary Matrix


Description
Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.
A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:
- All the visited cells of the path are
0. - All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).
The length of a clear path is the number of visited cells of this path.
Example 1:
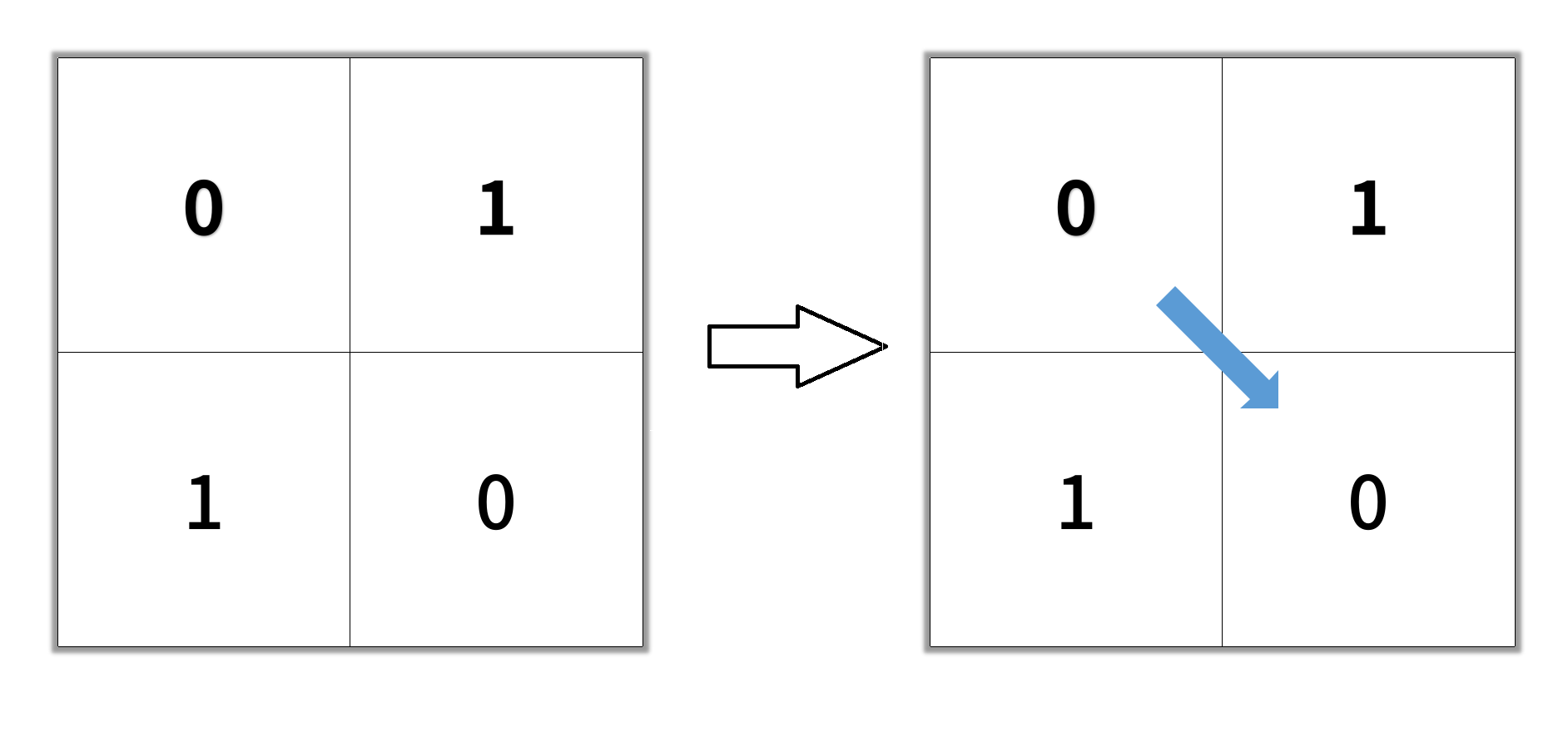
Input: grid = [[0,1],[1,0]] Output: 2
Example 2:
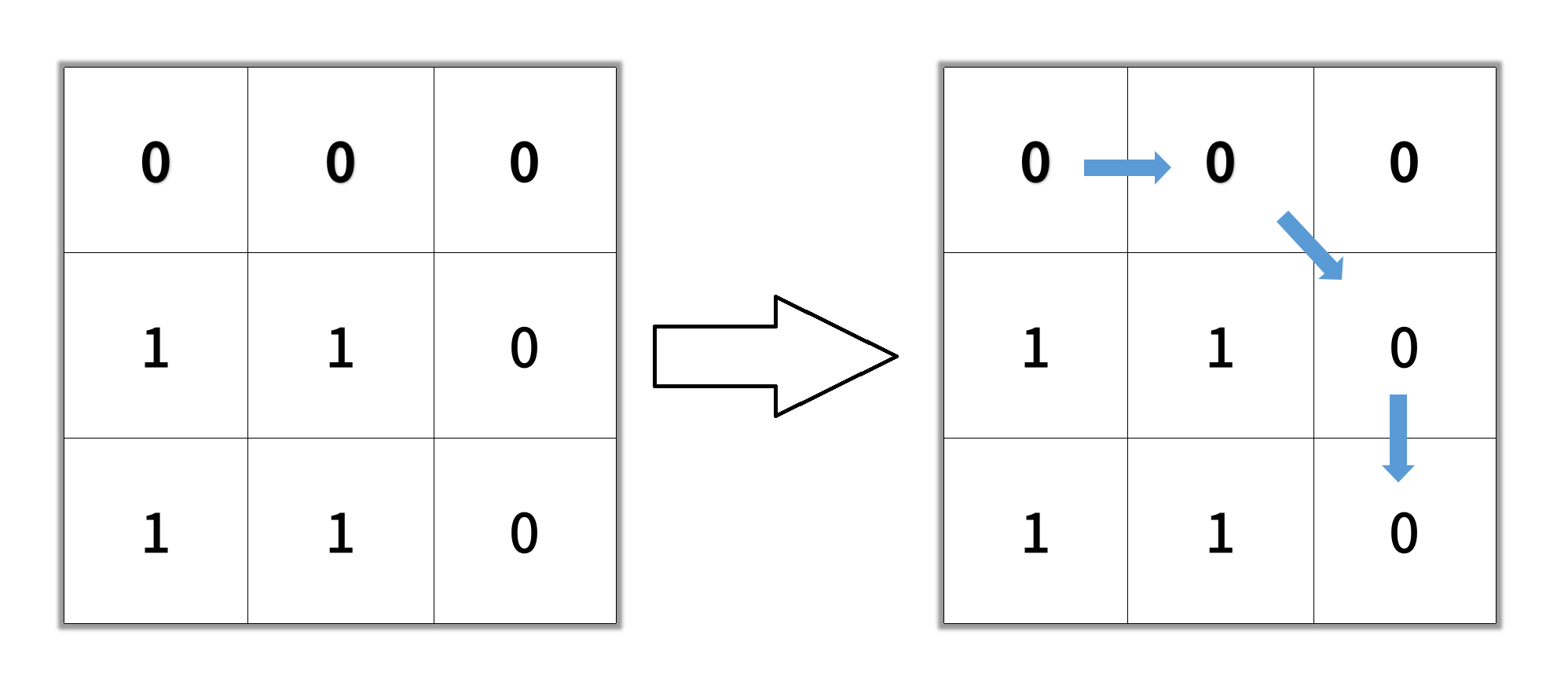
Input: grid = [[0,0,0],[1,1,0],[1,1,0]] Output: 4
Example 3:
Input: grid = [[1,0,0],[1,1,0],[1,1,0]] Output: -1
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j] is 0 or 1
Solution
shortest-path-in-binary-matrix.py
class Solution:
def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
if grid[0][0] == 1: return -1
rows, cols = len(grid), len(grid[0])
queue = deque([(0, 0, 1)])
grid[0][0] = 1
while queue:
x, y, steps = queue.popleft()
if x == rows - 1 and y == cols - 1:
return steps
for dx in range(x - 1, x + 2):
for dy in range(y - 1, y + 2):
if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] == 0:
grid[dx][dy] = 1
queue.append((dx, dy, steps + 1))
return -1