1130. Minimum Cost Tree From Leaf Values


Description
Given an array arr of positive integers, consider all binary trees such that:
- Each node has either
0or2children; - The values of
arrcorrespond to the values of each leaf in an in-order traversal of the tree. - The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree, respectively.
Among all possible binary trees considered, return the smallest possible sum of the values of each non-leaf node. It is guaranteed this sum fits into a 32-bit integer.
A node is a leaf if and only if it has zero children.
Example 1:
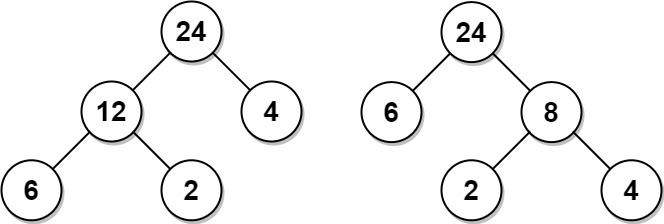
Input: arr = [6,2,4] Output: 32 Explanation: There are two possible trees shown. The first has a non-leaf node sum 36, and the second has non-leaf node sum 32.
Example 2:
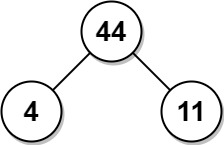
Input: arr = [4,11] Output: 44
Constraints:
2 <= arr.length <= 401 <= arr[i] <= 15- It is guaranteed that the answer fits into a 32-bit signed integer (i.e., it is less than 231).
Solution
minimum-cost-tree-from-leaf-values.py
class Solution:
def mctFromLeafValues(self, arr: List[int]) -> int:
res = 0
while len(arr) > 1:
index = arr.index(min(arr))
if 0 < index < len(arr) - 1:
res += arr[index] * min(arr[index + 1], arr[index - 1])
else:
res += arr[index] * (arr[index + 1] if index == 0 else arr[index - 1])
arr.pop(index)
return res