1192. Critical Connections in a Network

Description
There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [ai, bi] represents a connection between servers ai and bi. Any server can reach other servers directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some servers unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
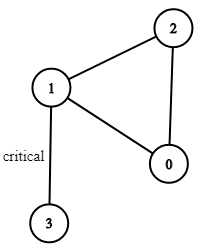
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]] Output: [[1,3]] Explanation: [[3,1]] is also accepted.
Example 2:
Input: n = 2, connections = [[0,1]] Output: [[0,1]]
Constraints:
2 <= n <= 105n - 1 <= connections.length <= 1050 <= ai, bi <= n - 1ai != bi- There are no repeated connections.
Solution
critical-connections-in-a-network.py
class Solution:
def criticalConnections(self, n, connections):
def makeGraph(connections):
graph = collections.defaultdict(list)
for conn in connections:
graph[conn[0]].append(conn[1])
graph[conn[1]].append(conn[0])
return graph
graph = makeGraph(connections)
connections = set(map(tuple, (map(sorted, connections))))
rank = [-2] * n
def dfs(node, depth):
if rank[node] >= 0:
# visiting (0<=rank<n), or visited (rank=n)
return rank[node]
rank[node] = depth
min_back_depth = n
for neighbor in graph[node]:
if rank[neighbor] == depth - 1:
continue # don't immmediately go back to parent. that's why i didn't choose -1 as the special value, in case depth==0.
back_depth = dfs(neighbor, depth + 1)
if back_depth <= depth:
connections.discard(tuple(sorted((node, neighbor))))
min_back_depth = min(min_back_depth, back_depth)
rank[node] = n # this line is not necessary. see the "brain teaser" section below
return min_back_depth
dfs(0, 0) # since this is a connected graph, we don't have to loop over all nodes.
return list(connections)