1326. Minimum Number of Taps to Open to Water a Garden


Description
There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).
There are n + 1 taps located at points [0, 1, ..., n] in the garden.
Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.
Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.
Example 1:
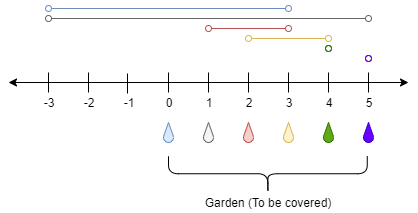
Input: n = 5, ranges = [3,4,1,1,0,0] Output: 1 Explanation: The tap at point 0 can cover the interval [-3,3] The tap at point 1 can cover the interval [-3,5] The tap at point 2 can cover the interval [1,3] The tap at point 3 can cover the interval [2,4] The tap at point 4 can cover the interval [4,4] The tap at point 5 can cover the interval [5,5] Opening Only the second tap will water the whole garden [0,5]
Example 2:
Input: n = 3, ranges = [0,0,0,0] Output: -1 Explanation: Even if you activate all the four taps you cannot water the whole garden.
Constraints:
1 <= n <= 104ranges.length == n + 10 <= ranges[i] <= 100
Solution
minimum-number-of-taps-to-open-to-water-a-garden.py
class Solution:
def minTaps(self, n: int, ranges: List[int]) -> int:
A = [0] * (n + 1)
for i, x in enumerate(ranges):
if x == 0: continue
left = max(i - x, 0)
A[left] = max(A[left], i + x)
jumps = currStep = currFarthest = i = 0
while i < len(A) and currStep < n:
jumps += 1
while i < len(A) and i <= currStep:
currFarthest = max(currFarthest, A[i])
i += 1
if currStep == currFarthest: return -1
currStep = currFarthest
return jumps