1368. Minimum Cost to Make at Least One Valid Path in a Grid

,%20Matrix,%20Shortest%20Path-orange.svg)
Description
Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:
1which means go to the cell to the right. (i.e go fromgrid[i][j]togrid[i][j + 1])2which means go to the cell to the left. (i.e go fromgrid[i][j]togrid[i][j - 1])3which means go to the lower cell. (i.e go fromgrid[i][j]togrid[i + 1][j])4which means go to the upper cell. (i.e go fromgrid[i][j]togrid[i - 1][j])
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.
Return the minimum cost to make the grid have at least one valid path.
Example 1:
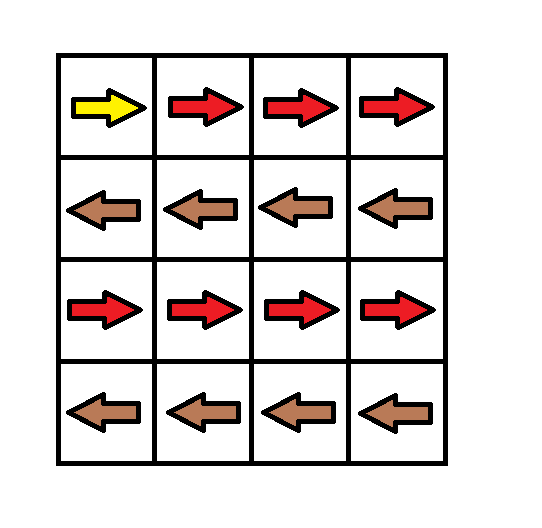
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]] Output: 3 Explanation: You will start at point (0, 0). The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3) The total cost = 3.
Example 2:
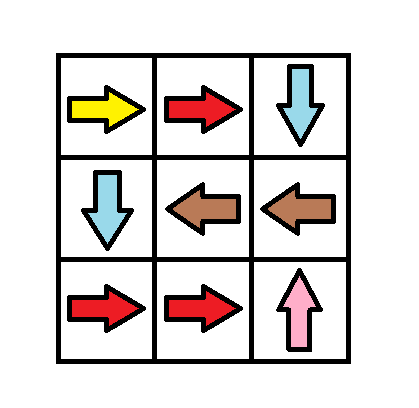
Input: grid = [[1,1,3],[3,2,2],[1,1,4]] Output: 0 Explanation: You can follow the path from (0, 0) to (2, 2).
Example 3:
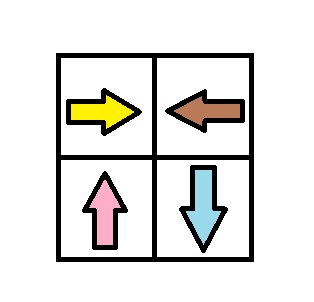
Input: grid = [[1,2],[4,3]] Output: 1
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1001 <= grid[i][j] <= 4
Solution
minimum-cost-to-make-at-least-one-valid-path-in-a-grid.py
class Solution:
def minCost(self, grid: List[List[int]]) -> int:
rows, cols = len(grid), len(grid[0])
dist = [[float('inf')] * cols for _ in range(rows)]
dist[0][0] = 0
d = [0, 1, 0, -1, 0]
def getNextSteps(x, y, k):
if k == 1:
i = 0
elif k == 2:
i = 2
elif k == 3:
i = 1
elif k == 4:
i = 3
return (x + d[i], y + d[i + 1])
queue = deque([(0, 0, 0)])
while queue:
costs, x, y = queue.popleft()
if costs != dist[x][y]: continue
if x == rows - 1 and y == cols - 1:
return costs
nx, ny = getNextSteps(x, y, grid[x][y])
for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
if 0 <= dx < rows and 0 <= dy < cols:
old = dist[dx][dy]
new = dist[x][y] + int(not (dx == nx and dy == ny))
if new < old:
dist[dx][dy] = new
if dx == nx and dy == ny:
queue.appendleft((new, dx, dy))
else:
queue.append((new, dx, dy))
return dist[-1][-1]