1568. Minimum Number of Days to Disconnect Island


Description
You are given an m x n binary grid grid where 1 represents land and 0 represents water. An island is a maximal 4-directionally (horizontal or vertical) connected group of 1's.
The grid is said to be connected if we have exactly one island, otherwise is said disconnected.
In one day, we are allowed to change any single land cell (1) into a water cell (0).
Return the minimum number of days to disconnect the grid.
Example 1:
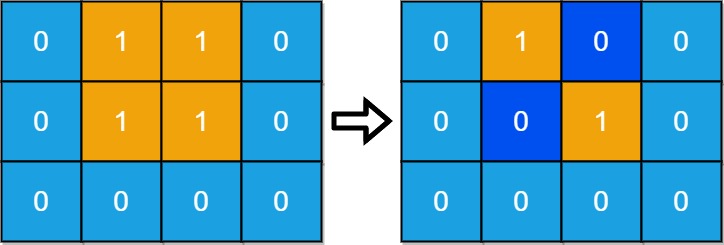
Input: grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]] Output: 2 Explanation: We need at least 2 days to get a disconnected grid. Change land grid[1][1] and grid[0][2] to water and get 2 disconnected island.
Example 2:

Input: grid = [[1,1]] Output: 2 Explanation: Grid of full water is also disconnected ([[1,1]] -> [[0,0]]), 0 islands.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j]is either0or1.
Solution
minimum-number-of-days-to-disconnect-island.py
import copy
class Solution:
#this is just a helper function for the no_islands function below
def no_islands_recur(self, grid, i, j, m, n):
if grid[i][j]==0:
return
grid[i][j]=0
if i-1>=0:
self.no_islands_recur(grid, i-1, j, m, n)
if i+1<m:
self.no_islands_recur(grid, i+1, j, m, n)
if j-1>=0:
self.no_islands_recur(grid, i, j-1, m, n)
if j+1<n:
self.no_islands_recur(grid, i, j+1, m, n)
#find how many islands the given grid has
def no_islands(self, grid):
ret = 0
m, n = len(grid), len(grid[0])
for i in range(m):
for j in range(n):
if grid[i][j] == 1:
ret += 1
self.no_islands_recur(grid, i, j, m, n)
return ret
def minDays(self, grid: List[List[int]]) -> int:
#if we have 0 or more than 1 islands at day 0, return day 0
time = 0
grid_copy = copy.deepcopy(grid)
n = self.no_islands(grid_copy)
if n!=1:
return time
#try to remove any land any see if it works
time = 1
for i in range(len(grid)):
for j in range(len(grid[0])):
grid_copy = copy.deepcopy(grid)
grid_copy[i][j] = 0
n = self.no_islands(grid_copy)
if n!=1:
return time
#well then just return 2
time = 2
return time