1914. Cyclically Rotating a Grid


Description
You are given an m x n integer matrix grid, where m and n are both even integers, and an integer k.
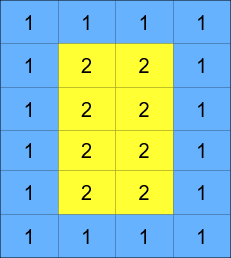
The matrix is composed of several layers, which is shown in the below image, where each color is its own layer:
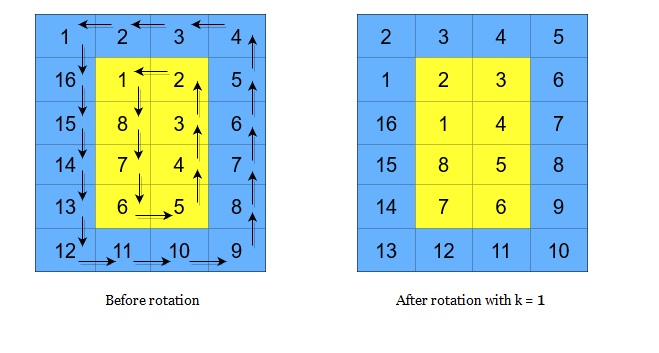
A cyclic rotation of the matrix is done by cyclically rotating each layer in the matrix. To cyclically rotate a layer once, each element in the layer will take the place of the adjacent element in the counter-clockwise direction. An example rotation is shown below:
Return the matrix after applying k cyclic rotations to it.
Example 1:
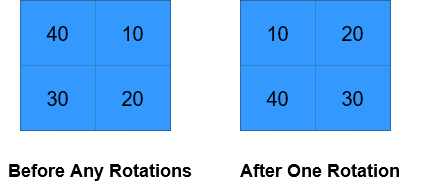
Input: grid = [[40,10],[30,20]], k = 1 Output: [[10,20],[40,30]] Explanation: The figures above represent the grid at every state.
Example 2:
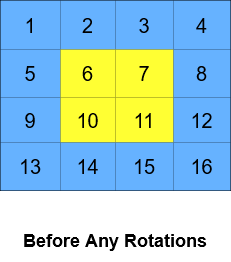
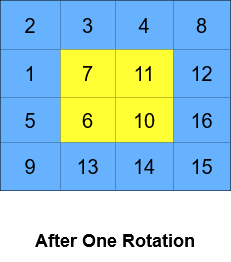
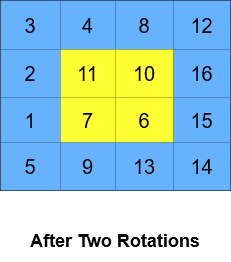
Input: grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2 Output: [[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]] Explanation: The figures above represent the grid at every state.
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 50- Both
mandnare even integers. 1 <= grid[i][j] <= 50001 <= k <= 109
Solution
cyclically-rotating-a-grid.py
class Solution:
def rotateGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
rows, cols = len(grid), len(grid[0])
for r in range(min(rows, cols) // 2):
i = j = r
vals = []
for jj in range(j, cols - j - 1):
vals.append(grid[i][jj])
for ii in range(i, rows - i - 1):
vals.append(grid[ii][cols - j - 1])
for jj in range(cols - j - 1, j, -1):
vals.append(grid[rows - i - 1][jj])
for ii in range(rows - i - 1, i, -1):
vals.append(grid[ii][j])
kk = k % len(vals)
vals = vals[kk:] + vals[:kk]
x = 0
for jj in range(j, cols - j - 1):
grid[i][jj] = vals[x]; x += 1
for ii in range(i, rows - i - 1):
grid[ii][cols - j - 1] = vals[x]; x += 1
for jj in range(cols - j - 1, j, -1):
grid[rows - i - 1][jj] = vals[x]; x += 1
for ii in range(rows - i - 1, i, -1):
grid[ii][j] = vals[x]; x += 1
return grid