2002. Maximum Product of the Length of Two Palindromic Subsequences

Description

Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.

Return the maximum possible product of the lengths of the two palindromic subsequences.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.

 

Example 1:

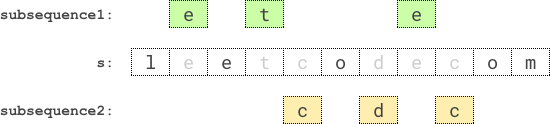
Input: s = "leetcodecom"
Output: 9
Explanation: An optimal solution is to choose "ete" for the 1st subsequence and "cdc" for the 2nd subsequence.
The product of their lengths is: 3 * 3 = 9.

Example 2:

Input: s = "bb"
Output: 1
Explanation: An optimal solution is to choose "b" (the first character) for the 1st subsequence and "b" (the second character) for the 2nd subsequence.
The product of their lengths is: 1 * 1 = 1.

Example 3:

Input: s = "accbcaxxcxx"
Output: 25
Explanation: An optimal solution is to choose "accca" for the 1st subsequence and "xxcxx" for the 2nd subsequence.
The product of their lengths is: 5 * 5 = 25.

 

Constraints:

• 2 <= s.length <= 12
• s consists of lowercase English letters only.

Solution

maximum-product-of-the-length-of-two-palindromic-subsequences.py

class Solution:
    def maxProduct(self, s: str) -> int:
        n = len(s)
        N = 1 << n
        A = []

        for mask in range(1, N):
            subseq = ''
            for i in range(n):
                if (mask >> i) & 1:
                    subseq += s[i]

            if subseq == subseq[::-1]:
                A.append((mask, len(subseq)))

        A.sort(key = lambda x:-x[1])
        res = 1
        for i in range(len(A)):
            mask1, len1 = A[i]
            if len1 ** 2 < res: break

            for j in range(i + 1, len(A)):
                mask2, len2 = A[j]
                if mask1 & mask2 == 0 and len1 * len2 > res:
                    res = len1 * len2
                    break

        return res