2132. Stamping the Grid


Description
You are given an m x n binary matrix grid where each cell is either 0 (empty) or 1 (occupied).
You are then given stamps of size stampHeight x stampWidth. We want to fit the stamps such that they follow the given restrictions and requirements:
- Cover all the empty cells.
- Do not cover any of the occupied cells.
- We can put as many stamps as we want.
- Stamps can overlap with each other.
- Stamps are not allowed to be rotated.
- Stamps must stay completely inside the grid.
Return true if it is possible to fit the stamps while following the given restrictions and requirements. Otherwise, return false.
Example 1:
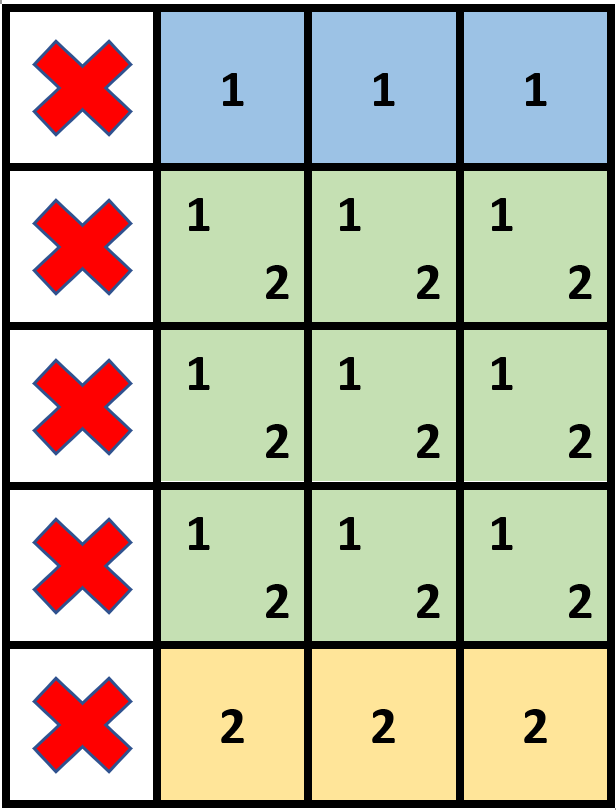
Input: grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3 Output: true Explanation: We have two overlapping stamps (labeled 1 and 2 in the image) that are able to cover all the empty cells.
Example 2:
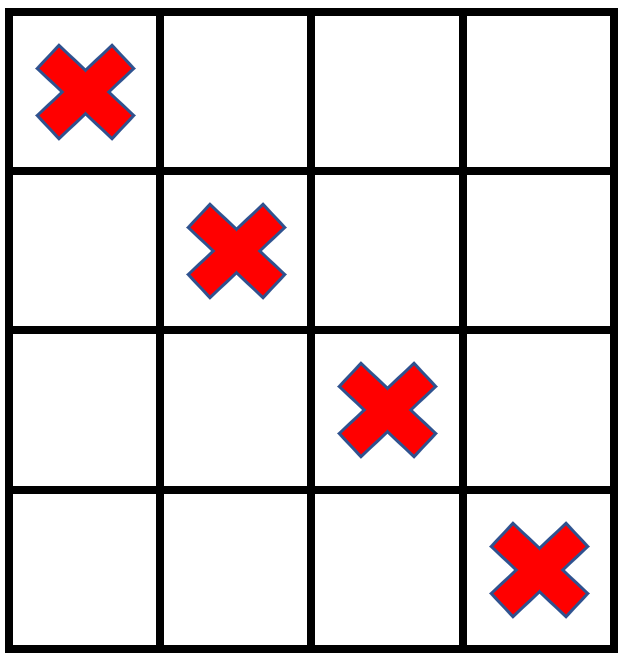
Input: grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 Output: false Explanation: There is no way to fit the stamps onto all the empty cells without the stamps going outside the grid.
Constraints:
m == grid.lengthn == grid[r].length1 <= m, n <= 1051 <= m * n <= 2 * 105grid[r][c]is either0or1.1 <= stampHeight, stampWidth <= 105
Solution
stamping-the-grid.py
class Solution:
def possibleToStamp(self, grid: List[List[int]], H: int, W: int) -> bool:
rows, cols = len(grid), len(grid[0])
prefix = [[0] * (cols + 1) for _ in range(rows + 1)]
for i in range(rows):
for j in range(cols):
prefix[i + 1][j + 1] = prefix[i][j + 1] + prefix[i + 1][j] - prefix[i][j] + grid[i][j]
diff = [[0] * (cols + 1) for _ in range(rows + 1)]
for i in range(rows - H + 1):
for j in range(cols - W + 1):
count = prefix[i + H][j + W] - prefix[i][j + W] - prefix[i + H][j] + prefix[i][j]
if count == 0:
diff[i][j] += 1
diff[i][j + W] -= 1
diff[i + H][j] -= 1
diff[i + H][j + W] += 1
for i in range(rows + 1):
for j in range(cols):
diff[i][j + 1] += diff[i][j]
for j in range(cols + 1):
for i in range(rows):
diff[i + 1][j] += diff[i][j]
for i in range(rows):
for j in range(cols):
if grid[i][j] == 0 and diff[i][j] == 0:
return False
return True