2146. K Highest Ranked Items Within a Price Range

Description

You are given a 0-indexed 2D integer array grid of size m x n that represents a map of the items in a shop. The integers in the grid represent the following:

• 0 represents a wall that you cannot pass through.
• 1 represents an empty cell that you can freely move to and from.
• All other positive integers represent the price of an item in that cell. You may also freely move to and from these item cells.

It takes 1 step to travel between adjacent grid cells.

You are also given integer arrays pricing and start where pricing = [low, high] and start = [row, col] indicates that you start at the position (row, col) and are interested only in items with a price in the range of [low, high] (inclusive). You are further given an integer k.

You are interested in the positions of the k highest-ranked items whose prices are within the given price range. The rank is determined by the first of these criteria that is different:

1. Distance, defined as the length of the shortest path from the start (shorter distance has a higher rank).
2. Price (lower price has a higher rank, but it must be in the price range).
3. The row number (smaller row number has a higher rank).
4. The column number (smaller column number has a higher rank).

Return the k highest-ranked items within the price range sorted by their rank (highest to lowest). If there are fewer than k reachable items within the price range, return all of them.

 

Example 1:

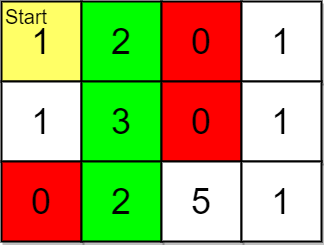
Input: grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
Output: [[0,1],[1,1],[2,1]]
Explanation: You start at (0,0).
With a price range of [2,5], we can take items from (0,1), (1,1), (2,1) and (2,2).
The ranks of these items are:
- (0,1) with distance 1
- (1,1) with distance 2
- (2,1) with distance 3
- (2,2) with distance 4
Thus, the 3 highest ranked items in the price range are (0,1), (1,1), and (2,1).

Example 2:

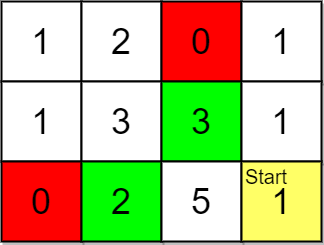
Input: grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
Output: [[2,1],[1,2]]
Explanation: You start at (2,3).
With a price range of [2,3], we can take items from (0,1), (1,1), (1,2) and (2,1).
The ranks of these items are:
- (2,1) with distance 2, price 2
- (1,2) with distance 2, price 3
- (1,1) with distance 3
- (0,1) with distance 4
Thus, the 2 highest ranked items in the price range are (2,1) and (1,2).

Example 3:

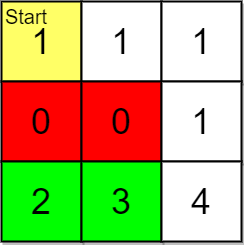
Input: grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
Output: [[2,1],[2,0]]
Explanation: You start at (0,0).
With a price range of [2,3], we can take items from (2,0) and (2,1). 
The ranks of these items are: 
- (2,1) with distance 5
- (2,0) with distance 6
Thus, the 2 highest ranked items in the price range are (2,1) and (2,0). 
Note that k = 3 but there are only 2 reachable items within the price range.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 0 <= grid[i][j] <= 105
• pricing.length == 2
• 2 <= low <= high <= 105
• start.length == 2
• 0 <= row <= m - 1
• 0 <= col <= n - 1
• grid[row][col] > 0
• 1 <= k <= m * n

Solution

k-highest-ranked-items-within-a-price-range.py

class Solution:
    def highestRankedKItems(self, grid: List[List[int]], pricing: List[int], start: List[int], k: int) -> List[List[int]]:
        rows, cols = len(grid), len(grid[0])
        heap = []
        sx, sy = start
        minP, maxP = pricing
        queue = deque([(sx, sy, 0)])
        visited = set([(sx, sy)])

        while queue:
            x, y, distance = queue.popleft()

            price = grid[x][y]

            if price != 1 and minP <= price <= maxP:
                if len(heap) == k:
                    heapq.heappushpop(heap, (-distance, -price, -x, -y))
                else:
                    heapq.heappush(heap, (-distance, -price, -x, -y))

            for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] != 0 and (dx, dy) not in visited:
                    queue.append((dx, dy, distance + 1))
                    visited.add((dx, dy))

        return [[-x, -y] for _, _, x, y in sorted(heap, reverse = 1)]