2258. Escape the Spreading Fire

Description

You are given a 0-indexed 2D integer array grid of size m x n which represents a field. Each cell has one of three values:

• 0 represents grass,
• 1 represents fire,
• 2 represents a wall that you and fire cannot pass through.

You are situated in the top-left cell, (0, 0), and you want to travel to the safehouse at the bottom-right cell, (m - 1, n - 1). Every minute, you may move to an adjacent grass cell. After your move, every fire cell will spread to all adjacent cells that are not walls.

Return the maximum number of minutes that you can stay in your initial position before moving while still safely reaching the safehouse. If this is impossible, return -1. If you can always reach the safehouse regardless of the minutes stayed, return 109.

Note that even if the fire spreads to the safehouse immediately after you have reached it, it will be counted as safely reaching the safehouse.

A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).

 

Example 1:

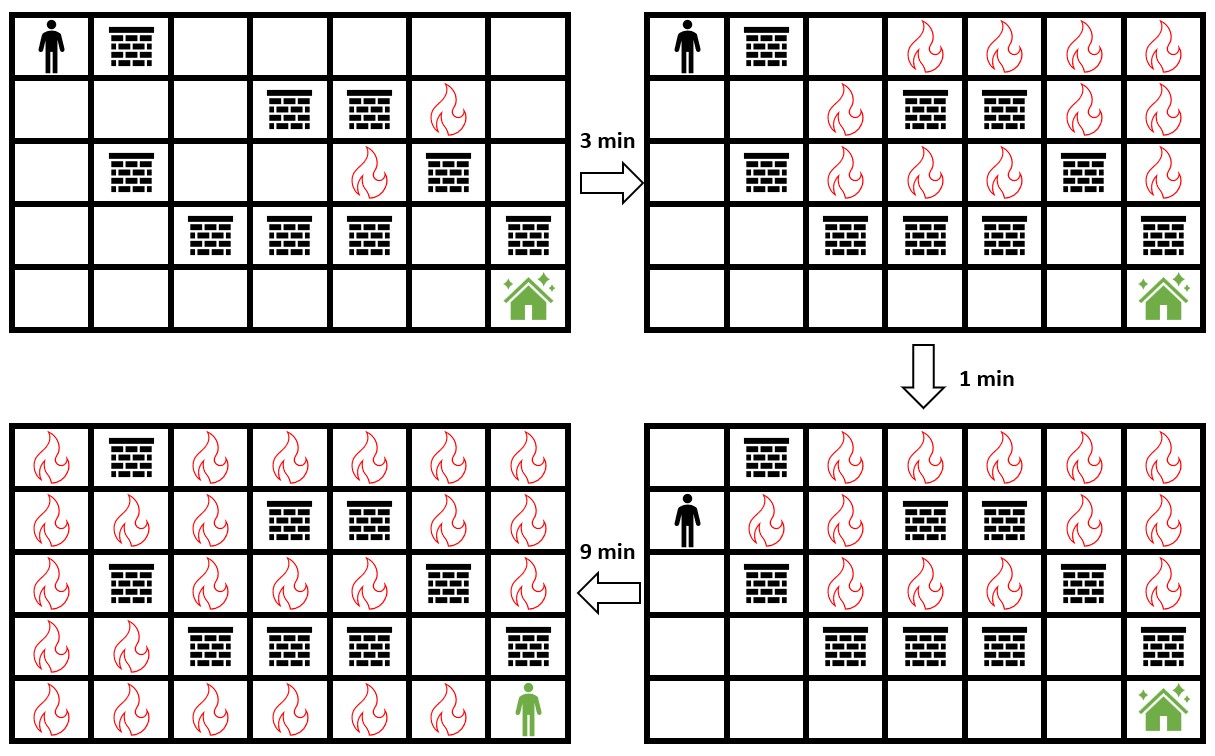
Input: grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]]
Output: 3
Explanation: The figure above shows the scenario where you stay in the initial position for 3 minutes.
You will still be able to safely reach the safehouse.
Staying for more than 3 minutes will not allow you to safely reach the safehouse.

Example 2:

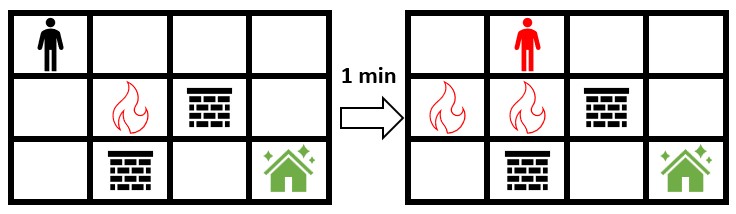
Input: grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]]
Output: -1
Explanation: The figure above shows the scenario where you immediately move towards the safehouse.
Fire will spread to any cell you move towards and it is impossible to safely reach the safehouse.
Thus, -1 is returned.

Example 3:

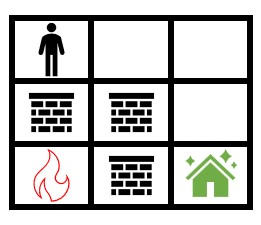
Input: grid = [[0,0,0],[2,2,0],[1,2,0]]
Output: 1000000000
Explanation: The figure above shows the initial grid.
Notice that the fire is contained by walls and you will always be able to safely reach the safehouse.
Thus, 109 is returned.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 300
• 4 <= m * n <= 2 * 104
• grid[i][j] is either 0, 1, or 2.
• grid[0][0] == grid[m - 1][n - 1] == 0

Solution

escape-the-spreading-fire.py

class Solution:
    def maximumMinutes(self, grid: List[List[int]]) -> int:
        rows, cols = len(grid), len(grid[0])
        INF = 10 ** 10
        dist = [[INF] * cols for _ in range(rows)]
        fire = deque()

        for x in range(rows):
            for y in range(cols):
                if grid[x][y] == 1:
                    dist[x][y] = 0
                    fire.append((0, x, y))

        while fire:
            d, x, y = fire.popleft()

            for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] != 2 and dist[dx][dy] == INF:
                    dist[dx][dy] = d + 1
                    fire.append((d + 1, dx, dy))

        def good(k):
            if dist[0][0] <= k: return False

            queue = deque([(k, 0, 0)])
            visited = [[False] * cols for _ in range(rows)]

            while queue:
                d, x, y = queue.popleft()

                for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                    if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] != 2 and not visited[dx][dy] and d + 1 < dist[dx][dy]:
                        visited[dx][dy] = True
                        queue.append((d + 1, dx, dy))

                        if dx == rows - 1 and dy == cols - 1: 
                            return True

                    if dx == rows - 1 and dy == cols - 1 and grid[dx][dy] != 2 and not visited[dx][dy] and d + 1 <= dist[dx][dy]: 
                        return True


            return False

        left, right = 0, 10 ** 9

        while left < right:
            mid = (left + right + 1) // 2

            if good(mid):
                left = mid
            else:
                right = mid - 1

        if left == 0:
            return 0 if good(0) else -1

        return left