2322. Minimum Score After Removals on a Tree

Description

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the i^th node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

Remove two distinct edges of the tree to form three connected components. For a pair of removed edges, the following steps are defined:

Get the XOR of all the values of the nodes for each of the three components respectively.
The difference between the largest XOR value and the smallest XOR value is the score of the pair.

For example, say the three components have the node values: [4,5,7], [1,9], and [3,3,3]. The three XOR values are 4 ^ 5 ^ 7 = 6, 1 ^ 9 = 8, and 3 ^ 3 ^ 3 = 3. The largest XOR value is 8 and the smallest XOR value is 3. The score is then 8 - 3 = 5.

Return the minimum score of any possible pair of edge removals on the given tree.

Example 1:

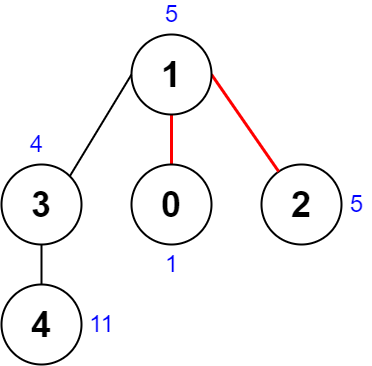
Input: nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
Output: 9
Explanation: The diagram above shows a way to make a pair of removals.
- The 1^st component has nodes [1,3,4] with values [5,4,11]. Its XOR value is 5 ^ 4 ^ 11 = 10.
- The 2^nd component has node [0] with value [1]. Its XOR value is 1 = 1.
- The 3^rd component has node [2] with value [5]. Its XOR value is 5 = 5.
The score is the difference between the largest and smallest XOR value which is 10 - 1 = 9.
It can be shown that no other pair of removals will obtain a smaller score than 9.

Example 2:

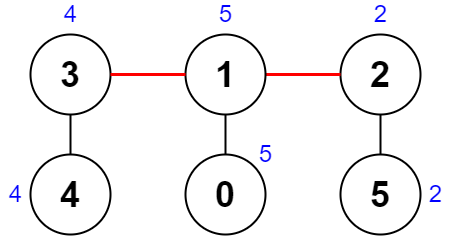
Input: nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
Output: 0
Explanation: The diagram above shows a way to make a pair of removals.
- The 1^st component has nodes [3,4] with values [4,4]. Its XOR value is 4 ^ 4 = 0.
- The 2^nd component has nodes [1,0] with values [5,5]. Its XOR value is 5 ^ 5 = 0.
- The 3^rd component has nodes [2,5] with values [2,2]. Its XOR value is 2 ^ 2 = 0.
The score is the difference between the largest and smallest XOR value which is 0 - 0 = 0.
We cannot obtain a smaller score than 0.

Constraints:

n == nums.length
3 <= n <= 1000
1 <= nums[i] <= 10⁸
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges represents a valid tree.

Solution

minimum-score-after-removals-on-a-tree.py

class Solution:
    def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
        N, M = len(nums), len(edges)

        graph = defaultdict(list)
        children = defaultdict(set)
        xor = nums.copy()
        V = 0
        degree = [0] * N

        for a, b in edges:
            graph[a].append(b)
            graph[b].append(a)
            degree[a] += 1
            degree[b] += 1

        seen = set()
        dq = deque()

        for node in range(N):
            V ^= nums[node]
            if degree[node] == 1:
                dq.append(node)
                seen.add(node)

        while dq:
            node = dq.popleft()

            for nei in graph[node]:
                if nei not in seen:
                    children[nei].add(node)
                    children[nei] |= children[node]
                    xor[nei] ^= xor[node]

                degree[nei] -= 1

                if degree[nei] == 1:
                    dq.append(nei)
                    seen.add(nei)

        res = float('inf')

        for i in range(M - 1):
            for j in range(i + 1, M):
                a, b = edges[i]

                if b in children[a]:
                    a, b = b, a

                c, d = edges[j]

                if d in children[c]:
                    c, d = d, c

                if a in children[c]:
                    curr = [xor[a], xor[c] ^ xor[a], V ^ xor[c]]
                elif c in children[a]:
                    curr = [xor[c], xor[a] ^ xor[c], V ^ xor[a]]
                else:
                    curr = [xor[c], xor[a], V ^ xor[c] ^ xor[a]]

                res = min(res, max(curr) - min(curr))

        return res