2368. Reachable Nodes With Restrictions

Description

There is an undirected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 2D integer array edges of length n - 1 where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree. You are also given an integer array restricted which represents restricted nodes.

Return the maximum number of nodes you can reach from node 0 without visiting a restricted node.

Note that node 0 will not be a restricted node.

Example 1:

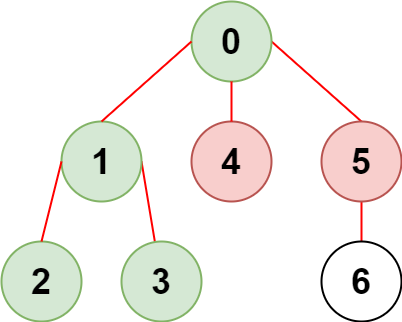
Input: n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
Output: 4
Explanation: The diagram above shows the tree.
We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.

Example 2:

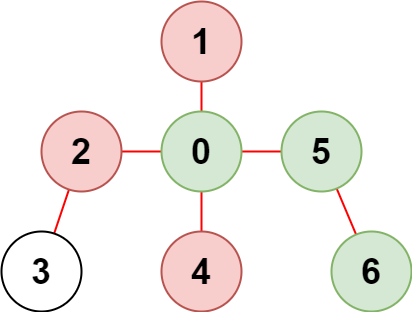
Input: n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
Output: 3
Explanation: The diagram above shows the tree.
We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.

Constraints:

2 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges represents a valid tree.
1 <= restricted.length < n
1 <= restricted[i] < n
All the values of restricted are unique.

Solution

reachable-nodes-with-restrictions.py

class Solution:
    def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:
        res = 0
        R = set(restricted)
        visited = set()
        G = defaultdict(list)

        for a, b in edges:
            G[a].append(b)
            G[b].append(a)

        def dfs(node):
            visited.add(node)

            for nei in G[node]:
                if nei not in R and nei not in visited:
                    dfs(nei)

        dfs(0)
        return len(visited)