2373. Largest Local Values in a Matrix


Description
You are given an n x n integer matrix grid.
Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:
maxLocal[i][j]is equal to the largest value of the3 x 3matrix ingridcentered around rowi + 1and columnj + 1.
In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.
Return the generated matrix.
Example 1:
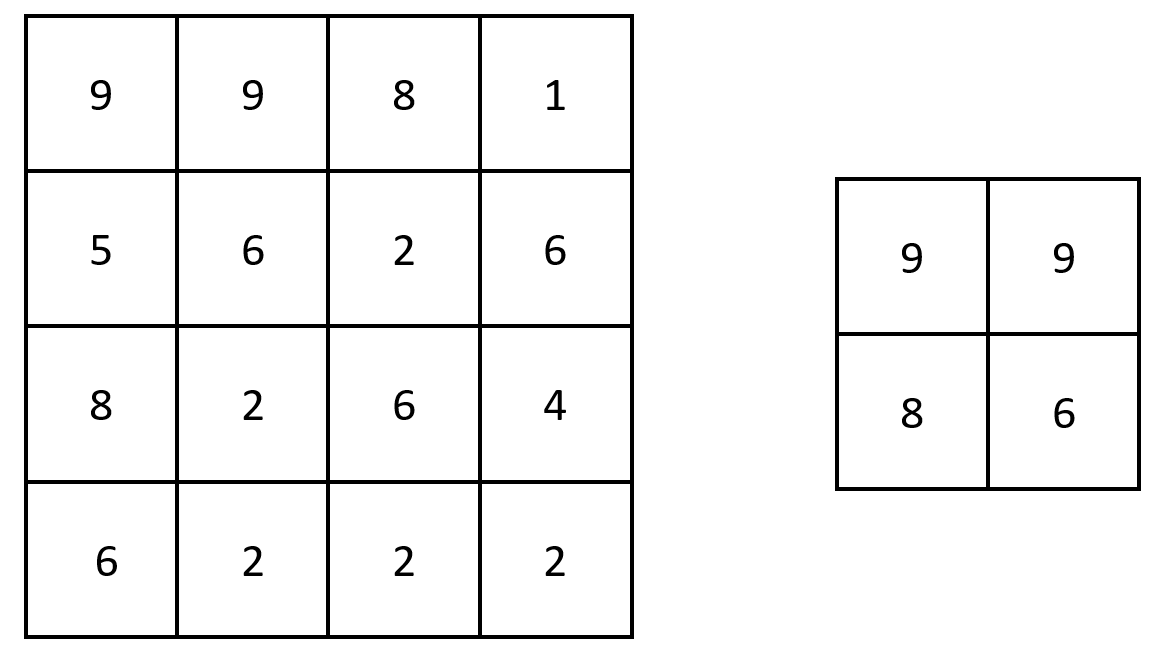
Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]] Output: [[9,9],[8,6]] Explanation: The diagram above shows the original matrix and the generated matrix. Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.
Example 2:
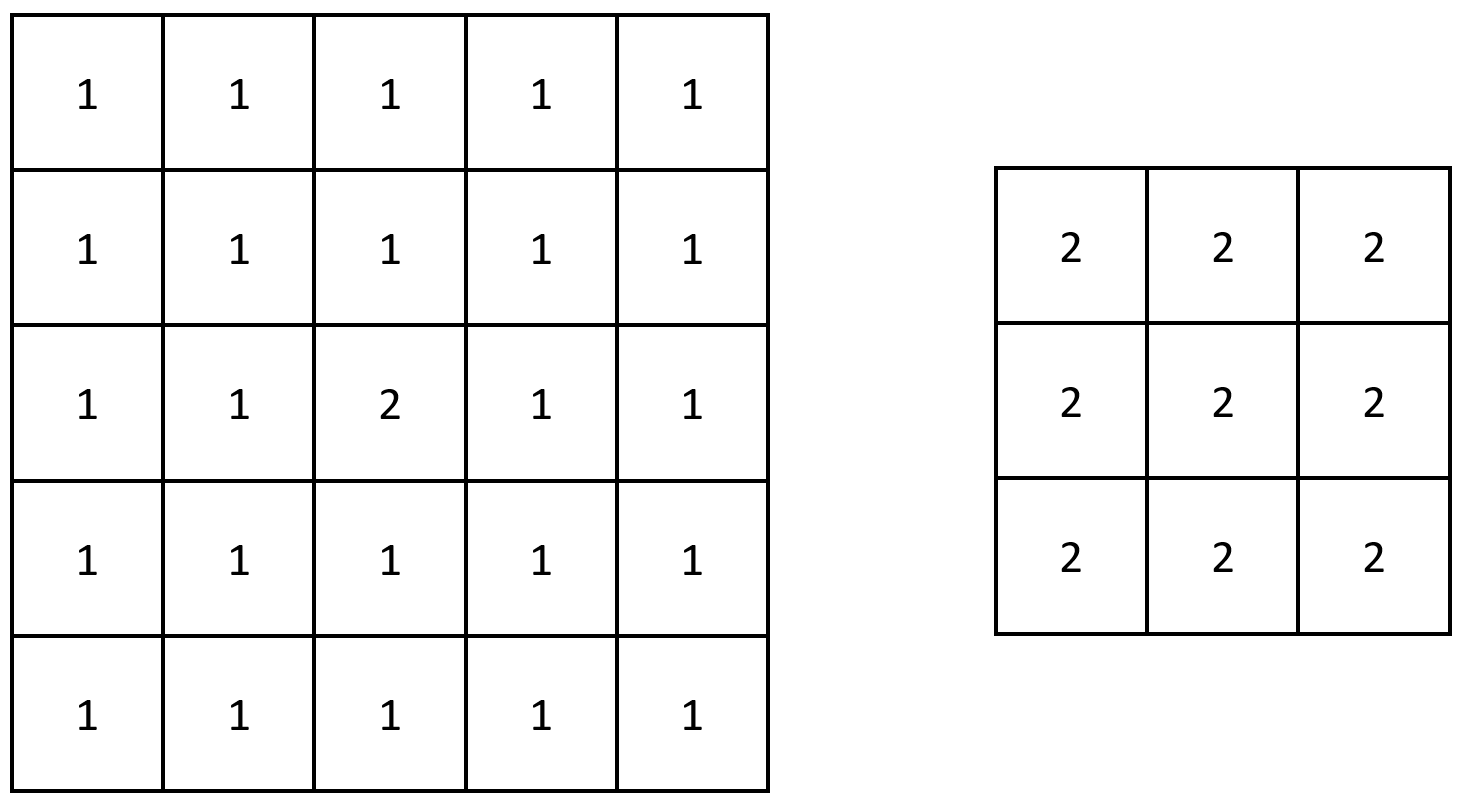
Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]] Output: [[2,2,2],[2,2,2],[2,2,2]] Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
Constraints:
n == grid.length == grid[i].length3 <= n <= 1001 <= grid[i][j] <= 100
Solution
largest-local-values-in-a-matrix.py
class Solution:
def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:
n = len(grid)
res = [[0] * (n - 2) for _ in range(n - 2)]
for i in range(n - 2):
for j in range(n - 2):
mmax = 0
for di in range(i, i + 3):
for dj in range(j, j + 3):
mmax = max(mmax, grid[di][dj])
res[i][j] = mmax
return res