2392. Build a Matrix With Conditions


Description
You are given a positive integer k. You are also given:
- a 2D integer array
rowConditionsof sizenwhererowConditions[i] = [abovei, belowi], and - a 2D integer array
colConditionsof sizemwherecolConditions[i] = [lefti, righti].
The two arrays contain integers from 1 to k.
You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.
The matrix should also satisfy the following conditions:
- The number
aboveishould appear in a row that is strictly above the row at which the numberbelowiappears for allifrom0ton - 1. - The number
leftishould appear in a column that is strictly left of the column at which the numberrightiappears for allifrom0tom - 1.
Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.
Example 1:
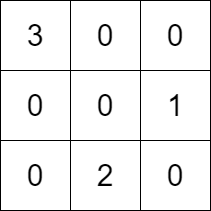
Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]] Output: [[3,0,0],[0,0,1],[0,2,0]] Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions. The row conditions are the following: - Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix. - Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix. The column conditions are the following: - Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix. - Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix. Note that there may be multiple correct answers.
Example 2:
Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]] Output: [] Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied. No matrix can satisfy all the conditions, so we return the empty matrix.
Constraints:
2 <= k <= 4001 <= rowConditions.length, colConditions.length <= 104rowConditions[i].length == colConditions[i].length == 21 <= abovei, belowi, lefti, righti <= kabovei != belowilefti != righti
Solution
build-a-matrix-with-conditions.py
class Solution:
def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:
res = [[0] * k for _ in range(k)]
def topoSort(A):
adj = [[] for _ in range(k + 1)]
for a, b in A:
adj[a].append(b)
seen = [False] * (k + 1)
order = []
def dfs(x):
if seen[x]: return
seen[x] = True
for nei in adj[x]:
if not seen[nei]:
dfs(nei)
order.append(x)
for x in range(1, k + 1):
dfs(x)
order.reverse()
M = {j: i for i, j in enumerate(order)}
if all(M[i] < M[j] for i, j in A):
return order
return None
R = topoSort(rowConditions)
C = topoSort(colConditions)
if R is None or C is None:
return []
RM = {j : i for i, j in enumerate(R)}
CM = {j : i for i, j in enumerate(C)}
for x in range(1, k + 1):
res[RM[x]][CM[x]] = x
return res