2435. Paths in Matrix Whose Sum Is Divisible by K


Description
You are given a 0-indexed m x n integer matrix grid and an integer k. You are currently at position (0, 0) and you want to reach position (m - 1, n - 1) moving only down or right.
Return the number of paths where the sum of the elements on the path is divisible by k. Since the answer may be very large, return it modulo 109 + 7.
Example 1:
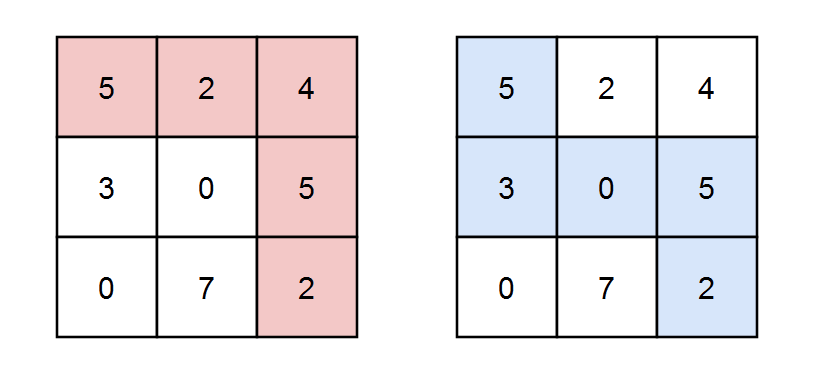
Input: grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3 Output: 2 Explanation: There are two paths where the sum of the elements on the path is divisible by k. The first path highlighted in red has a sum of 5 + 2 + 4 + 5 + 2 = 18 which is divisible by 3. The second path highlighted in blue has a sum of 5 + 3 + 0 + 5 + 2 = 15 which is divisible by 3.
Example 2:
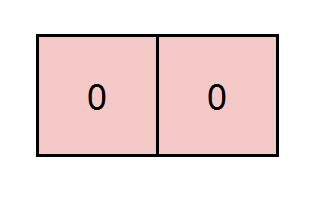
Input: grid = [[0,0]], k = 5 Output: 1 Explanation: The path highlighted in red has a sum of 0 + 0 = 0 which is divisible by 5.
Example 3:
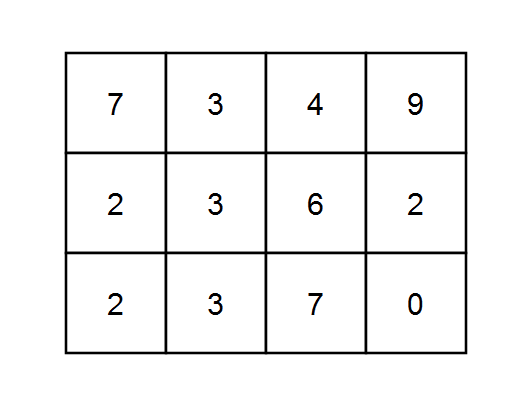
Input: grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1 Output: 10 Explanation: Every integer is divisible by 1 so the sum of the elements on every possible path is divisible by k.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 5 * 1041 <= m * n <= 5 * 1040 <= grid[i][j] <= 1001 <= k <= 50
Solution
paths-in-matrix-whose-sum-is-divisible-by-k.py
M = 10 ** 9 + 7
class Solution:
def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
rows, cols = len(grid), len(grid[0])
dp = [[[0] * k for _ in range(cols)] for _ in range(rows)]
dp[0][0][grid[0][0] % k] = 1
for i in range(rows):
for j in range(cols):
for kk in range(k):
dp[i][j][kk] %= M
if i + 1 < rows:
dp[i + 1][j][(grid[i + 1][j] + kk) % k] += dp[i][j][kk]
if j + 1 < cols:
dp[i][j + 1][(grid[i][j + 1] + kk) % k] += dp[i][j][kk]
return dp[rows - 1][cols - 1][0]
paths-in-matrix-whose-sum-is-divisible-by-k.cpp
class Solution {
public:
const long long M = 1e9 + 7;
int numberOfPaths(vector<vector<int>>& grid, int k) {
int rows = grid.size(), cols = grid[0].size();
long long cache[rows][cols][k];
memset(cache, -1, sizeof(cache));
function<long long(int, int, int)> go = [&](int i, int j, int curr) {
if (cache[i][j][curr] != -1) return cache[i][j][curr];
if (i == rows - 1 && j == cols - 1) return (long long)(curr == 0);
long long count = 0;
if (i + 1 < rows) {
count += go(i + 1, j, (curr + grid[i + 1][j]) % k);
count %= M;
}
if (j + 1 < cols) {
count += go(i, j + 1, (curr + grid[i][j + 1]) % k);
count %= M;
}
return cache[i][j][curr] = count;
};
return go(0, 0, grid[0][0] % k);
}
};