2440. Create Components With Same Value


Description
There is an undirected tree with n nodes labeled from 0 to n - 1.
You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the ith node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
You are allowed to delete some edges, splitting the tree into multiple connected components. Let the value of a component be the sum of all nums[i] for which node i is in the component.
Return the maximum number of edges you can delete, such that every connected component in the tree has the same value.
Example 1:
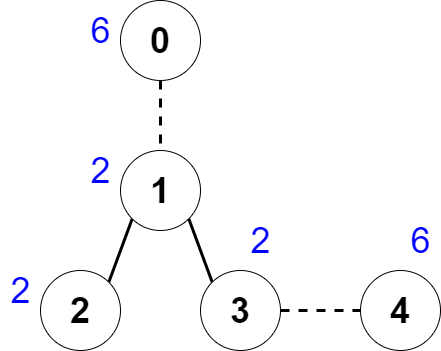
Input: nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]] Output: 2 Explanation: The above figure shows how we can delete the edges [0,1] and [3,4]. The created components are nodes [0], [1,2,3] and [4]. The sum of the values in each component equals 6. It can be proven that no better deletion exists, so the answer is 2.
Example 2:
Input: nums = [2], edges = [] Output: 0 Explanation: There are no edges to be deleted.
Constraints:
1 <= n <= 2 * 104nums.length == n1 <= nums[i] <= 50edges.length == n - 1edges[i].length == 20 <= edges[i][0], edges[i][1] <= n - 1edgesrepresents a valid tree.
Solution
create-components-with-same-value.py
class Solution:
def componentValue(self, nums: List[int], edges: List[List[int]]) -> int:
N = len(nums)
graph = defaultdict(list)
total = sum(nums)
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
def good(divisor):
if total % divisor != 0: return False
target = total // divisor
count = 0
visited = [False] * N
def dfs(node):
nonlocal count
if visited[node]: return 0
visited[node] = True
curr = nums[node]
for nei in graph[node]:
curr += dfs(nei)
if curr == target:
count += 1
curr = 0
return curr
dfs(0)
return count == divisor
for divisor in range(N, 0, -1):
if good(divisor):
return divisor - 1
return 0