2458. Height of Binary Tree After Subtree Removal Queries


Description
You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.
You have to perform m independent queries on the tree where in the ith query you do the following:
- Remove the subtree rooted at the node with the value
queries[i]from the tree. It is guaranteed thatqueries[i]will not be equal to the value of the root.
Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.
Note:
- The queries are independent, so the tree returns to its initial state after each query.
- The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.
Example 1:
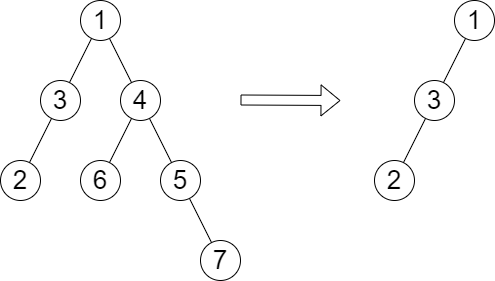
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4] Output: [2] Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4. The height of the tree is 2 (The path 1 -> 3 -> 2).
Example 2:
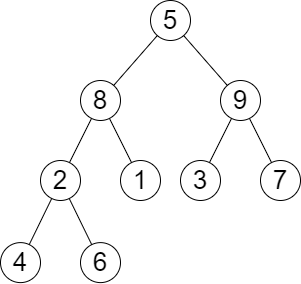
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8] Output: [3,2,3,2] Explanation: We have the following queries: - Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4). - Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1). - Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6). - Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).
Constraints:
- The number of nodes in the tree is
n. 2 <= n <= 1051 <= Node.val <= n- All the values in the tree are unique.
m == queries.length1 <= m <= min(n, 104)1 <= queries[i] <= nqueries[i] != root.val
Solution
height-of-binary-tree-after-subtree-removal-queries.py
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def treeQueries(self, root: Optional[TreeNode], queries: List[int]) -> List[int]:
D = {}
H = {}
def go(node, depth):
if not node: return -1
D[node.val] = depth
height = 1 + max(go(node.left, depth + 1), go(node.right, depth + 1))
H[node.val] = height
return height
go(root, 0)
levels = defaultdict(list)
for node, depth in D.items():
if len(levels[depth]) == 2:
heappushpop(levels[depth], (H[node], node))
else:
heappush(levels[depth], (H[node], node))
res = []
for node in queries:
depth = D[node]
if len(levels[depth]) == 1:
res.append(depth - 1)
elif levels[depth][1][1] == node:
res.append(levels[depth][0][0] + depth)
else:
res.append(levels[depth][1][0] + depth)
return res