2492. Minimum Score of a Path Between Two Cities

Description

You are given a positive integer n representing n cities numbered from 1 to n. You are also given a 2D array roads where roads[i] = [a_i, b_i, distance_i] indicates that there is a bidirectional road between cities a_i and b_i with a distance equal to distance_i. The cities graph is not necessarily connected.

The score of a path between two cities is defined as the minimum distance of a road in this path.

Return the minimum possible score of a path between cities 1 and n.

Note:

A path is a sequence of roads between two cities.
It is allowed for a path to contain the same road multiple times, and you can visit cities 1 and n multiple times along the path.
The test cases are generated such that there is at least one path between 1 and n.

Example 1:

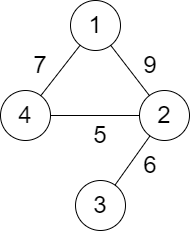
Input: n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
Output: 5
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 4. The score of this path is min(9,5) = 5.
It can be shown that no other path has less score.

Example 2:

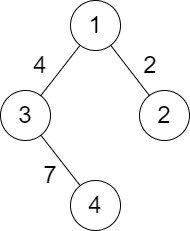
Input: n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
Output: 2
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 1 -> 3 -> 4. The score of this path is min(2,2,4,7) = 2.

Constraints:

2 <= n <= 10⁵
1 <= roads.length <= 10⁵
roads[i].length == 3
1 <= a_i, b_i <= n
a_i != b_i
1 <= distance_i <= 10⁴
There are no repeated edges.
There is at least one path between 1 and n.

Solution

minimum-score-of-a-path-between-two-cities.py

class Solution:
    def minScore(self, N: int, roads: List[List[int]]) -> int:
        graph = defaultdict(list)

        for a, b, dist in roads:
            graph[a].append((b, dist))
            graph[b].append((a, dist))

        res = inf

        stack = [1]
        visited = set(stack)

        while stack:
            node = stack.pop()

            for nei, dist in graph[node]:
                res = min(res, dist)

                if nei in visited: continue

                visited.add(nei)
                stack.append(nei)

        return res