2493. Divide Nodes Into the Maximum Number of Groups

Description

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [a_i,b_i] indicates that there is a bidirectional edge between nodes a_i and b_i. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

Each node in the graph belongs to exactly one group.
For every pair of nodes in the graph that are connected by an edge [a_i,b_i], if a_i belongs to the group with index x, and b_i belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

Example 1:

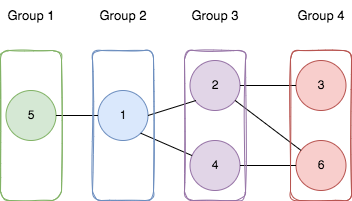
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Output: 4
Explanation: As shown in the image we:
- Add node 5 to the first group.
- Add node 1 to the second group.
- Add nodes 2 and 4 to the third group.
- Add nodes 3 and 6 to the fourth group.
We can see that every edge is satisfied.
It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
It can be shown that no grouping is possible.

Constraints:

1 <= n <= 500
1 <= edges.length <= 10⁴
edges[i].length == 2
1 <= a_i, b_i <= n
a_i != b_i
There is at most one edge between any pair of vertices.

Solution

divide-nodes-into-the-maximum-number-of-groups.py

def is_bipartite(graph, n):
    color = defaultdict(int)

    def go(x):
        for node in graph[x]:
            if node not in color:
                color[node] = -color[x]
                if not go(node):
                    return False
            else:
                if color[x] == color[node]:
                    return False

        return True

    for i in range(n):
        if i not in color:
            color[i] = 1
            if not go(i):
                return False

    return True


class Solution:
    def magnificentSets(self, N: int, edges: List[List[int]]) -> int:
        graph = defaultdict(list)

        for a, b in edges:
            a -= 1
            b -= 1
            graph[a].append(b)
            graph[b].append(a)

        if not is_bipartite(graph, N): return -1

        groups = []
        grouped = set()

        for node in range(N):
            if node in grouped: continue

            group = set([node])
            stack = [node]

            while stack:
                curr = stack.pop()

                for nei in graph[curr]:
                    if nei in group: continue
                    group.add(nei)
                    stack.append(nei)

            groups.append(group)
            grouped |= group

        res = 0
        for group in groups:
            maxDepth = 0

            for start in group:
                depth = {}
                depth[start] = 0
                queue = deque([start])

                while queue:
                    node = queue.popleft()

                    for nei in graph[node]:
                        if nei in depth: continue

                        depth[nei] = depth[node] + 1
                        queue.append(nei)

                maxDepth = max(maxDepth, max(depth.values()))

            res += maxDepth + 1

        return res