2503. Maximum Number of Points From Grid Queries

Description

You are given an m x n integer matrix grid and an array queries of size k.

Find an array answer of size k such that for each integer queres[i] you start in the top left cell of the matrix and repeat the following process:

If queries[i] is strictly greater than the value of the current cell that you are in, then you get one point if it is your first time visiting this cell, and you can move to any adjacent cell in all 4 directions: up, down, left, and right.
Otherwise, you do not get any points, and you end this process.

After the process, answer[i] is the maximum number of points you can get. Note that for each query you are allowed to visit the same cell multiple times.

Return the resulting array answer.

Example 1:

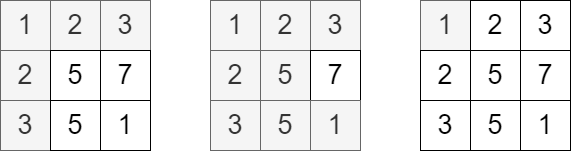
Input: grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
Output: [5,8,1]
Explanation: The diagrams above show which cells we visit to get points for each query.

Example 2:

Input: grid = [[5,2,1],[1,1,2]], queries = [3]
Output: [0]
Explanation: We can not get any points because the value of the top left cell is already greater than or equal to 3.

Constraints:

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 10⁵
k == queries.length
1 <= k <= 10⁴
1 <= grid[i][j], queries[i] <= 10⁶

Solution

maximum-number-of-points-from-grid-queries.py

class Solution:
    def maxPoints(self, grid: List[List[int]], queries: List[int]) -> List[int]:
        rows, cols = len(grid), len(grid[0])
        res = []
        pq = [(grid[0][0], 0, 0)]
        grid[0][0] = 0
        orders = []
        currMax = -1

        while pq:
            val, x, y = heappop(pq)
            currMax = max(currMax, val)
            orders.append(currMax)

            for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] != 0:
                    heappush(pq, (grid[dx][dy], dx, dy))
                    grid[dx][dy] = 0

        for q in queries:
            res.append(bisect_left(orders, q))

        return res