2508. Add Edges to Make Degrees of All Nodes Even

Description

There is an undirected graph consisting of n nodes numbered from 1 to n. You are given the integer n and a 2D array edges where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i. The graph can be disconnected.

You can add at most two additional edges (possibly none) to this graph so that there are no repeated edges and no self-loops.

Return true if it is possible to make the degree of each node in the graph even, otherwise return false.

The degree of a node is the number of edges connected to it.

Example 1:

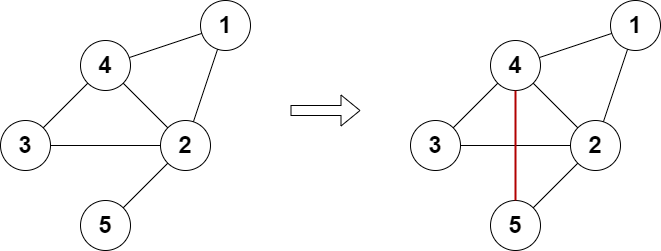
Input: n = 5, edges = [[1,2],[2,3],[3,4],[4,2],[1,4],[2,5]]
Output: true
Explanation: The above diagram shows a valid way of adding an edge.
Every node in the resulting graph is connected to an even number of edges.

Example 2:

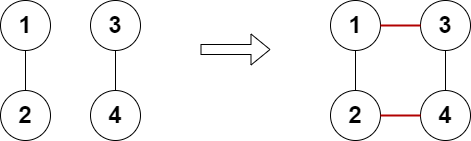
Input: n = 4, edges = [[1,2],[3,4]]
Output: true
Explanation: The above diagram shows a valid way of adding two edges.

Example 3:

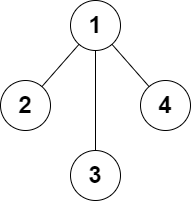
Input: n = 4, edges = [[1,2],[1,3],[1,4]]
Output: false
Explanation: It is not possible to obtain a valid graph with adding at most 2 edges.

Constraints:

3 <= n <= 10⁵
2 <= edges.length <= 10⁵
edges[i].length == 2
1 <= a_i, b_i <= n
a_i != b_i
There are no repeated edges.

Solution

add-edges-to-make-degrees-of-all-nodes-even.py

class Solution:
    def isPossible(self, N: int, edges: List[List[int]]) -> bool:
        degree = [0] * N
        graph = [set() for _ in range(N)]

        for a, b in edges:
            a -= 1
            b -= 1
            degree[a] += 1
            degree[b] += 1
            graph[a].add(b)
            graph[b].add(a)

        odd_count = 0
        odds = []

        for i in range(N):
            if degree[i] % 2 == 1:
                odds.append(i)
                odd_count += 1

        if odd_count == 0: return True

        if odd_count == 2:
            a, b = odds

            if a not in graph[b]: return True

            for node in range(N):
                if node == a or node == b: continue

                if node not in graph[a] and node not in graph[b]:
                    return True

        elif odd_count == 4:
            for perm in permutations(odds, 4):
                a, b, c, d = list(perm)

                if a not in graph[b] and c not in graph[d]:
                    return True

        return False