2556. Disconnect Path in a Binary Matrix by at Most One Flip


Description
You are given a 0-indexed m x n binary matrix grid. You can move from a cell (row, col) to any of the cells (row + 1, col) or (row, col + 1) that has the value 1. The matrix is disconnected if there is no path from (0, 0) to (m - 1, n - 1).
You can flip the value of at most one (possibly none) cell. You cannot flip the cells (0, 0) and (m - 1, n - 1).
Return true if it is possible to make the matrix disconnect or false otherwise.
Note that flipping a cell changes its value from 0 to 1 or from 1 to 0.
Example 1:
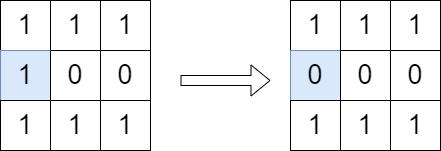
Input: grid = [[1,1,1],[1,0,0],[1,1,1]] Output: true Explanation: We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
Example 2:
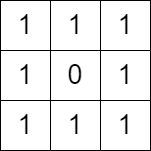
Input: grid = [[1,1,1],[1,0,1],[1,1,1]] Output: false Explanation: It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 105grid[i][j]is either0or1.grid[0][0] == grid[m - 1][n - 1] == 1
Solution
disconnect-path-in-a-binary-matrix-by-at-most-one-flip.py
class Solution:
def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:
rows, cols = len(grid), len(grid[0])
def dfs(x, y):
if x + 1 == rows and y + 1 == cols: return True
if x >= rows or y >= cols or grid[x][y] == 0: return False
grid[x][y] = 0
return dfs(x + 1, y) or dfs(x, y + 1)
if not dfs(0, 0): return True
grid[0][0] = 1
return not dfs(0, 0)
disconnect-path-in-a-binary-matrix-by-at-most-one-flip.cpp
class Solution {
public:
bool dfs(vector<vector<int>> &grid, int i, int j){
if(i+1 == grid.size() && j+1 == grid[0].size()) return true;
if(i >= grid.size() || j >= grid[0].size() || grid[i][j] == 0) return false;
grid[i][j] = 0;
return dfs(grid, i+1, j) || dfs(grid, i, j+1);
}
bool isPossibleToCutPath(vector<vector<int>>& grid) {
if(dfs(grid, 0, 0) == false) return true;
grid[0][0] = 1;
return !dfs(grid, 0, 0);
}
};